扩容方案出来后,之前文章 里提到的部分公式/结论已经失效,这里一一梳理下。
代码的改动
- RAM 扩容的细节可以看 官方源码,总结起来就是今后每出一个块新增 1KB 的 RAM 到可用 RAM 池子里。
- RAM 兑换公式里修正了 指数 的错误。不过这个修复也无伤大雅,因为可以看到通过 之前文章 里所写的推导过程,这个指数实际上最后会被约掉。新的代码依旧没有严格按照 bancor 算法白皮书 里写的公式来实现。其实这个也无关紧要,因为 EOS 并没有用到 bancor 算法的精华,仅仅是用来当作一个中间货币而已,其实本质上跟 bancor 没有任何关系。
bancor 白皮书第 11 页末尾里描述的公式为: 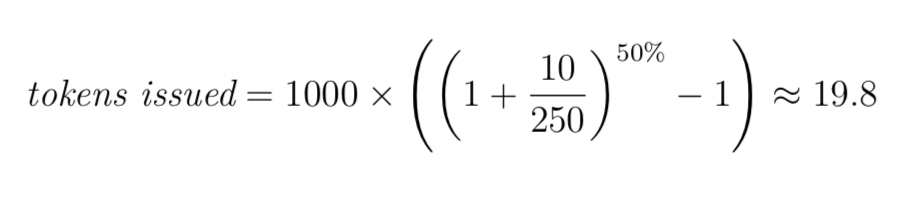
EOS 源码里实现的是: 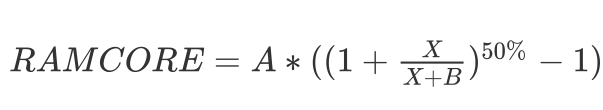
对比可以知道,区别在于分母这里,bancor 原始算法是用的更新前的值参与兑换,兑换完成后再更新值。而 EOS 的实现是先更新值,然后再代入到兑换公式里参与计算。
对之前结论的影响
尽管修正了指数,但是单位 EOS 兑换多少 RAM 的公式 依旧生效,因为上面说了推导过程中这个指数会被约掉,感兴趣的同学可以自己去试试。
\[ UnitEOSforRAM=\frac{C}{1+B}≈\frac{C}{B} \]
同理单位 RAM 兑换多少 EOS 的公式也有效:
\[ UnitRAMforEOS=\frac{B}{1+C}≈\frac{B}{C} \]
大家可以从现在的数据验证上面两个公式的正确性。
由于扩容方案的影响,之前得到的那个比较有趣的结论已经失效了:
无论RAM市场如何波动,B 和 C 的乘积是 几乎 保持不变的。
那么现在的 B 和 C 之积是什么呢,我尝试推导了一下。
还是以买入 RAM 为例,B、C 变化情况为:
\[ \begin{aligned} B_1 &= B_0 + X_0\\ C_1 &= C_0 - RAM+\Delta C_1 = \frac{B_0C_0}{X_0+B_0}+\Delta C_1 \end{aligned} \]
\(\Delta C_1\) 为这期间增发的 RAM 容量。继续:
\[ B_1C_1 = B_0C_0+B_1 \Delta C_1 \]
同样的:
\[ B_2C_2 = B_1C_1+B_2 \Delta C_2= B_0C_0+B_1 \Delta C_1+B_2 \Delta C_2 \]
即:
\[ B_nC_n = B_0C_0+B_1 \Delta C_1+B_2 \Delta C_2+…+B_n \Delta C_n \]
以写本篇文章的时刻为例,区块高度为 10912132: 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16{
"rows": [
{
"supply": "10000000000.0000 RAMCORE",
"base": {
"balance": "23715712979 RAM",
"weight": "0.50000000000000000"
},
"quote": {
"balance": "3712787.3588 EOS",
"weight": "0.50000000000000000"
}
}
],
"more": false
}
即此时的 \(B_n=3712787.3588\) , \(C_n=23715712979/1024=23159875.9560547\)。有:
\(B_nC_n=3712787.3588*23159875.9560547=85987694681015.95\)
据我所知,实施 RAM 扩容方案时的区块高度大概在 7827060 左右,那个时候的 B 和 C 是:\(B_0=4446923\) , \(C_0=15091077.8928\)
考虑到那时有个突然暴增 1.5G 内存的 bug,那么实际的 \(B_0C_0\) 应该是:
\(B_0C_0=(1.5*1024*1024+15091077.8928)*4446923=74103266473755.86\)
那么:
\[ \begin{aligned} &B_1 \Delta C_1+B_2 \Delta C_2+…+B_n \Delta C_n\\ =&B_nC_n-B_0C_0\\ =&85987694681015.95-74103266473755.86\\ =&11884428207260.1 \end{aligned} \]
而 \(\Delta C\) 为两笔 RAM 买卖之间增发的 RAM 容量,所以从 \(B_0\) 时刻到 \(B_n\) 时刻增发的 RAM 总容量即为两者的区块高度差乘以每个块增发的 RAM,即有:
\(\Delta C_1+\Delta C_2+...+\Delta C_n=(10912132-7827060)*1 KiB=3085072 KiB\)
本人纯野生数学爱好者,能力有限,业务繁忙,再加上马上想去拉个💩,就先在这里戛然而止了。