公式
以下公式推演参考 Bancor 白皮书
| 变量名 | 解释 |
|---|---|
| \(R\) | ETH 池子的储存量 |
| \(S\) | token 池子的储存量 |
| \(P\) | token 的即时单价(相对于 ETH) |
| \(F\) | 恒定的储备金比率,满足 \(F=R/(SP)\) |
我们的目标是求出当我要买 \(T\) 个 token 时,需要花费多少个 ETH,直觉告诉我们这个值应该是: \[ E=PT \tag{1} \]
因为 \(P\) 并不一定就是个常数,它会随着 token 储存量的变化而变化,所以更通用的写法应该是: \[ E=\int_{S_0}^{S_0+T}P \,{\rm d}S \tag{2} \]
于是我们想要求 \(E\) ,得先求出 \(P\) ,由 \(F\) 的定义有: \[ R=FSP \tag{3} \]
我们花费的 \(E\) 都是要进入到 \(R\) 的,那么由公式 \((2)\) 有: \[ {\rm d}R=P{\rm d}S \tag{4} \]
下面我们结合 $(3) $和 $(4) $:
\[ P\ {\rm d}S ={\rm d}R=F(S\ {\rm d}P+P\ {\rm d}S)\\ (1-F)P\ {\rm d}S =FS\ {\rm d}P\\ (\frac{1}{F}-1)P\ {\rm d}S =S\ {\rm d}P \tag{5} \]
由于 \(F\) 是一个常数,可以设 \(\alpha=\frac{1}{F}-1\) ,那么有:
\[ \alpha P\ {\rm d}S=S\ {\rm d}P\\ \alpha\frac{\ {\rm d}S}{S}=\frac{\ {\rm d}P}{P} \tag{6} \]
因为 \({(\ln{x})}^{'}=\frac{1}{x}\) ,有: \[ \alpha\ {\rm d}\ln{S}=\ {\rm d}\ln{P} \tag{7} \]
对上式两边同时积分: \[ \alpha\ln{S}+A=\ln{P} \tag{8} \]
接着稍微做些变换: \[ \ln{S^{\alpha}}+\ln{e^{A}}=\ln{P}\\ \ln{S^{\alpha}e^{A}}=\ln{P} \tag{9} \]
得到最终结果: \[ S^{\alpha}e^{A}=P \tag{10} \]
那么对于价格 \(P\) 的初始价格 \(P_0\) 和 token 的初始池子储存量 \(S_0\) 同样有: \[ {S_0}^{\alpha}e^{A}=P_0 \tag{11} \]
\((10)\) 和 \((11)\) 两式相除有: \[ P=(\frac{S}{S_0})^\alpha P_0 \tag{12} \]
至此,我们拿到了 \(P\) 的表达式,将其代入式 \((2)\) 有: \[ \begin{aligned} E&=\int_{S_0}^{S_0+T}P \,{\rm d}S\\ &=\int_{S_0}^{S_0+T}(\frac{S}{S_0})^{\alpha} P_0 \,{\rm d}S\\ &=\frac{P_0}{({S_0})^{\alpha}}\frac{({S})^{\alpha+1}}{\alpha+1}|_{S_0}^{S_0+T}\\ &=\int_{S_0}^{S_0+T}(\frac{P_0}{({S_0})^{\alpha}}) {S}^{\alpha} \,{\rm d}S\\ &=\frac{P_0}{\alpha+1}(\frac{({S_0+T})^{\alpha+1}}{({S_0})^{\alpha}}-S_0)\\ &=\frac{P_0S_0}{\alpha+1}(\frac{({S_0+T})^{\alpha+1}}{({S_0})^{\alpha+1}}-1)\\ &=\frac{P_0S_0}{\alpha+1}((1+\frac{T}{S_0})^{\alpha+1}-1) \end{aligned} \tag{13} \]
将 \(\alpha\) 还原至上式再将式子 \((3)\) 代入有: \[ \begin{aligned} E&=FP_0S_0((1+\frac{T}{S_0})^{\frac{1}{F}}-1)\\ &=R_0((1+\frac{T}{S_0})^{\frac{1}{F}}-1) \end{aligned} \tag{14} \]
上式就表示我要买 \(T\) 个 token 需要花费多少个 ETH,不过通常的场景应该是我用 \(E\) 个 ETH 能买到多少个 token,只需要把式子 \((13)\) 换下自变量和因变量: \[ T=S_0((1+\frac{E}{R_0})^{F}-1) \tag{15} \]
举例
鞭个尸,用我比较熟悉的 EOS 的内存模型来举例,公式 \((14)\) 在 EOS 的源码可以看到具体的实现,基本上这次是严格按照公式实现了(之前是
BM 自作聪明,添了点自己的想法,瞎改公式,参见旧版本代码)
另外我们可以利用式子 \((3)\) 倒推当时 EOS 的内存买卖模型刚上线的时候 RAM 的初始价格是多少:
\(R_0\) 和 \(S_0\) 的值可以从我的这篇文章里查到,这里直接贴结果:
\[ \begin{aligned} R_0&=1000000\ EOS\\ S_0&=64\cdot1024\cdot1024=67108864\ KB \end{aligned} \] 而 \(F\) 是写死的为 1,那么 RAM 刚上线时初始价格就是: \[ P_0=\frac{R_0}{FS_0}=\frac{1000000}{67108864}=0.014901161 \] 所以当时 RAM 的初始价格就是 0.014901161 EOS/KB,我们去区块浏览器上验证下这个数字对不对。验证方法也很简单,去找一个尽可能早的被 eosio 创建的一个始祖账号的交易 id,我这里随便找了一个存在区块高度为 1000 的交易,计算方法如图:
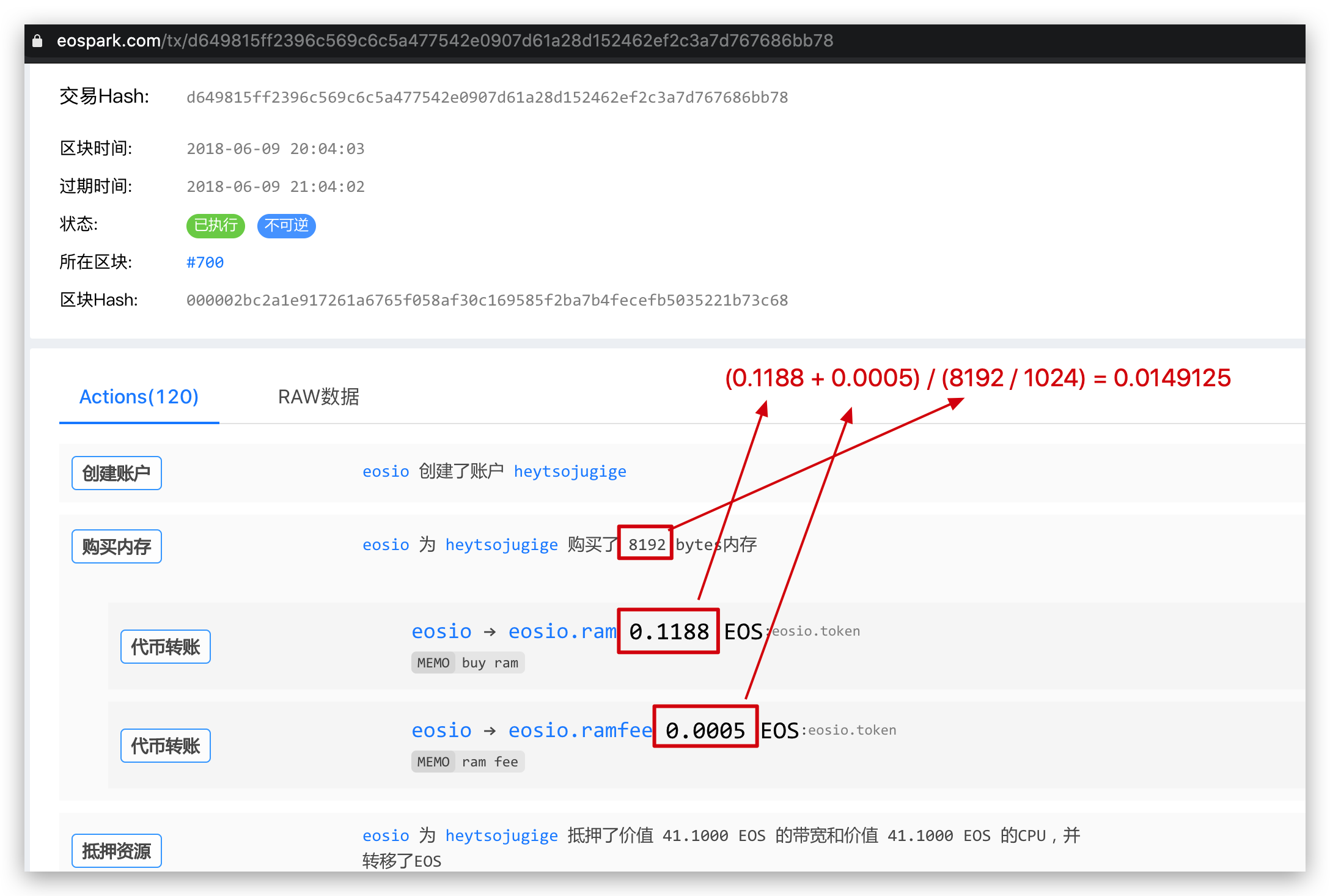
上图实际算出的值比 0.014901161 略大,是因为在这之前已经创建了不少账号了,如果你找到更早的被创建的始祖账号,按照上面的方法算出来的数字应该会更接近 0.014901161