公式
以下公式推演参考自 这里,不过本文剔除了一些乱七八糟的东西,精简了一部分推导过程
交易
投入指定数量的 A 代币应该得到多少个 B 代币
我们以 \(x\) 和 \(y\) 分别代表参与兑换的两种代币的池子储存量,当没有手续费的时候,有:
\[ x_1=x_0+\Delta x\\ y_1=y_0-\Delta y \]
由于已知的条件保证了:
\[ x_0y_0=x_1y_1 \]
整理上面三个式子后,有:
\[ x_1=x_0+\Delta x \]
\[ y_1=y_0-\Delta y=\frac{x_0y_0}{x_0+\Delta x} \]
如果 \(f\) 代表手续费,那么 \(y_1\) 就不一样了,设 \(y_1'\) 为修正后的 \(y_1\) :
\[ y_1^{'}=y_0-\Delta y=\frac{x_0y_0}{x_0+(1-f)\Delta x} \]
而我们要关心的 \(\Delta y\) 根据上式表达出来就是:
\[ \begin{aligned} \Delta y&=y_0-\frac{x_0y_0}{x_0+(1-f)\Delta x}\\ &=y_0(1-\frac{x_0}{x_0+(1-f)\Delta x})\\ &=\frac{(1-f)\Delta x y_0}{x_0+(1-f)\Delta x} \end{aligned} \]
目前手续费 \(f=0.003\) 代入计算有:
\[ \begin{aligned} \Delta y&=\frac{(1-0.003)\Delta x y_0}{x_0+(1-0.003)\Delta x}\\ &=\frac{0.997\Delta x y_0}{x_0+0.997\Delta x}\\ &=\frac{997\Delta x y_0}{1000x_0+997\Delta x} \end{aligned} \]
得出的这个公式和 源码 里写的是一样的。
想得到指定数量的 B 代币需要投入多少个 A 代币
跟上面的情况一样,只是整理出的式子需要变一下:
\[ x_1=x_0+\Delta x=\frac{x_0y_0}{y_0-\Delta y}\\ y_1=y_0-\Delta y \]
有:
\[ \begin{aligned} \Delta x&=\frac{x_0y_0}{y_0-\Delta y}-x_0\\ &=x_0(\frac{y_0}{y_0-\Delta y}-1)\\ &=\frac{x_0\Delta y}{y_0-\Delta y} \end{aligned} \]
但是要考虑到手续费的话,真正需要投入的 A 代币就应该满足:
\[ \begin{aligned} (1-f)\Delta x^{'}=\Delta x=\frac{x_0\Delta y}{y_0-\Delta y}\\ \Delta x^{'}=\frac{x_0\Delta y}{(1-f)(y_0-\Delta y)}=\frac{1000x_0\Delta y}{997(y_0-\Delta y)} \end{aligned} \]
跟 源码
写的公式基本一致,唯一不一样的地方是源码在最后的结果又
add(1) ,这个是为了防止算出来的 A 代币数值小于
1,导致手续费抽不出来,所以至少得付 1 个 B
代币(这里提到的代币数量都是精度放大后的值)。
铸币 UNI-V2
这里以注入流动性而铸币举例,根据 源码
可知,注入流动性的双方都是等比注入的,再加上 这里
铸币的逻辑可知铸币也同样是等比铸币的。以 s 表示 UNI-V2
的当前总储存量,那么就有:
\[ x_0 : y_0 : s_0=x_1 : y_1 : s_1 \]
设 \(k=xy\) 接着就有:
\[ \begin{aligned} \frac{k_1}{k_0}=\frac{x_1y_1}{x_0y_0}=(\frac{s_1}{s_0})^2 \end{aligned} \]
那么:
\[ \frac{s_1}{s_0}=\frac{\sqrt{k_1}}{\sqrt{k_0}}\\ \frac{s_2}{s_1}=\frac{\sqrt{k_2}}{\sqrt{k_1}}\\ …\\ \frac{s_n}{s_{n-1}}=\frac{\sqrt{k_n}}{\sqrt{k_{n-1}}} \]
以上各式累乘后有:
\[ \frac{s_n}{s_0}=\frac{\sqrt{k_n}}{\sqrt{k_0}} \]
而根据 源码 可知 \(s_0=\sqrt{k_0}\) ,变换并代入后:
\[ \begin{aligned} s_n-s_0&=(\sqrt{k_n}-\sqrt{k_0})\frac{s_0}{\sqrt{k_0}}=\sqrt{k_n}-\sqrt{k_0} \end{aligned} \]
那么通用地,很容易得出,在任意两个时刻 \(i\) 和 \(j\) 之间累计的手续费公式为:
\[ \begin{aligned} \Delta s_{ij}=&s_{i}-s_{j}\\ =&(s_{i}-s_{0})-(s_{j}-s_{0})\\ =&(\sqrt{k_i}-\sqrt{k_0})-(\sqrt{k_j}-\sqrt{k_0})\\ =&\sqrt{k_i}-\sqrt{k_j} \end{aligned} \]
然而现在 UniSwap
项目方没有打开收费开关,当开启收费后为了不影响现有持股人利益,必须按当前的持币比例增发对应数量的
UNI-V2 。如果开关打开后,设应该对 UniSwap 项目方增发的
UNI-V2 数量为 \(\Delta s\)
,项目方准备收取手续费里的比例为 \(F\)
(当前这个版本这个 \(F=1/6\)),那么就必须要满足:
\[ \begin{aligned} \frac{\Delta s}{\Delta s+s_0}=F\frac{\sqrt{k_1}-\sqrt{k_0}}{\sqrt{k_1}} \end{aligned} \]
表示成 \(\Delta s\) ,并代入 \(F=1/6\) 有:
\[ \begin{aligned} \Delta s =\frac{\sqrt{k_1}-\sqrt{k_0}}{(\frac{1}{F}-1)\sqrt{k_1}+\sqrt{k_0}}s_0=\frac{\sqrt{k_1}-\sqrt{k_0}}{5\sqrt{k_1}+\sqrt{k_0}}s_0 \end{aligned} \]
这个公式跟 源码 也是一致的。
好了,几个有代表性的公式就是这么推导出来的了,大家也不用害怕闷头抄代码心里不踏实了,项目方也可以安心出去骗钱了。
UPDATE
源码
里有一处我觉得应该是个 bug 的地方,下图那行里面传的参数应该是
balance0 和 balance1 才对: 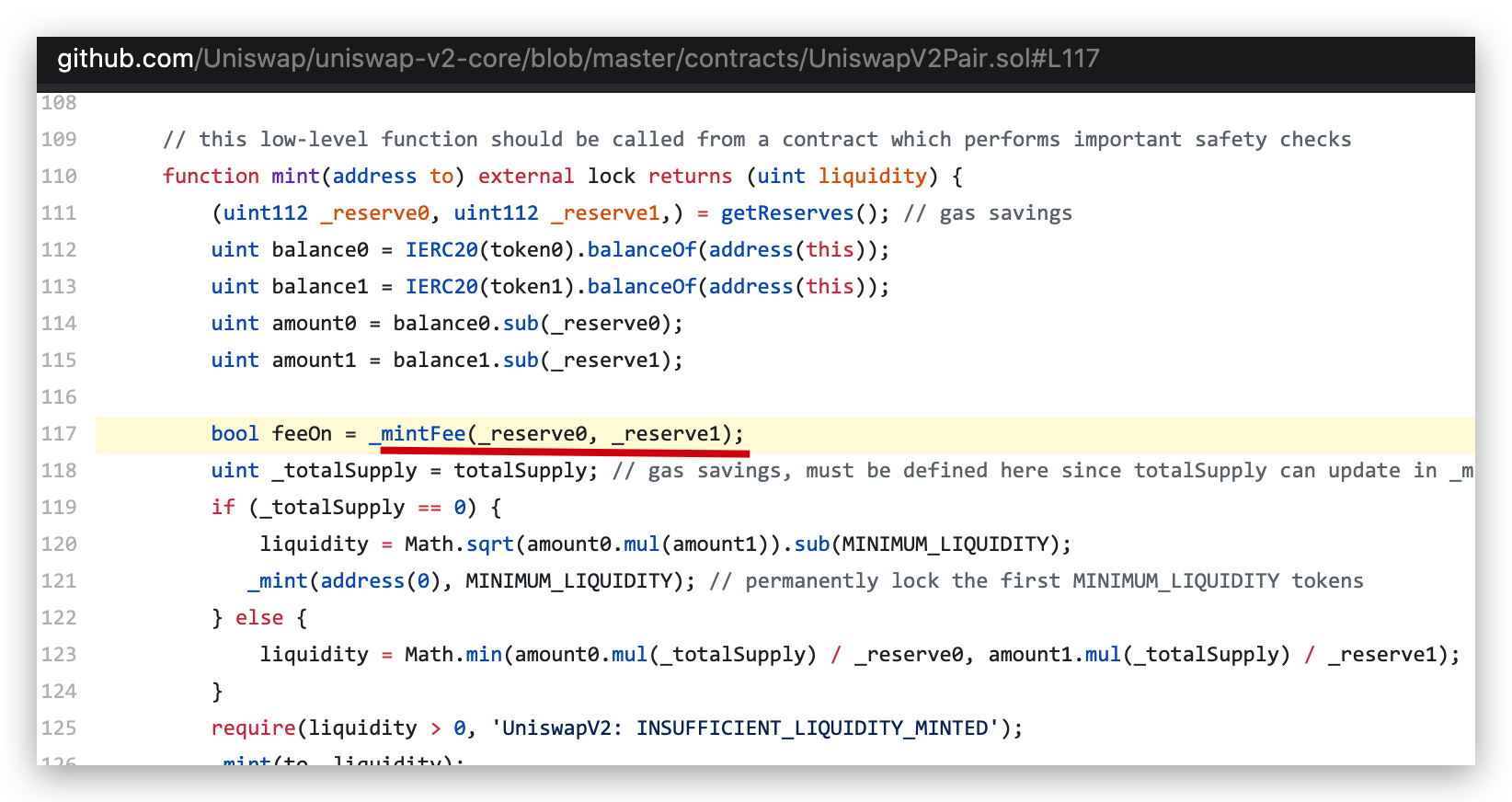
目前暂时不会对所有人造成影响,后续唯一会影响的是 UniSwap 项目方,因为即便某一天他们打开收费开关,因为这个 bug,他们也应该是收不到每笔交易里的 .05% 手续费的。
经过万圈朋友指点,这里没有 bug,swap 函数会更新储存量的,只有当连续发生两次注入流动性的时候才会复现这个问题,算是一个小瑕疵,不影响大局