我为什么讨厌助记词

Specer

2022-11-20

blockchain, thought

背景知识

熟悉我的人都知道我一向讨厌助记词，我觉得它的存在性价比不高。本文就从底层原理分析开始，解释为什么我觉得助记词很鸡肋。我这里只分析其中比较重要的三个跟助记词相关的 BIP

BIP32

主要目的

该 BIP 解决了由一个给定的（随机）数 entropy 推导出一系列子孙私钥/公钥的理论可能

前景知识

私钥的本质就是一个 32 字节的数
公钥的本质就是一个点（私钥点乘 G 的结果），一般都会将其序列化表示出来，x 坐标和 y 坐标各 32 字节，又由于椭圆曲线是关于 x 轴对称的，所以需要多一个字节表示奇偶性（y 的正负）显式地指明是哪一个点。所以完整的公钥表示需要 65 个字节，后来由于椭圆曲线的参数是固定的，可以直接由 x 计算出 y ，于是也可以用 33 个字节简要表示公钥（省去了表示 y 的 32 个字节）

详细的看下 BTC/ETH 签名机制简介

原文精简版

介绍了几个推导方法：

父私钥推导子私钥

$CKDpriv((k\_{par}, c\_{par}), i) → (k\_i, c\_i)$

检查 $i$ 的值
1. 如果 $i$ 是硬化的（$i ≥ 2^{31}$），$I = HMAC-SHA512(Key = c_{par}, Data = 0x00 || ser_{256}(k_{par}) || ser_{32}(i))$
2. 否则 $I = HMAC-SHA512(Key = c_{par}, Data = ser_P(point(k_{par})) || ser_{32}(i))$
将 $I$ 等分成两个 32 字节：$I_L$ 和 $I_R$
$k_i = parse_{256}(I_L) + k_{par} (\mod\ n)$
$c_i = I_R$
$assert(parse_{256}(I_L) < n \ \&\&\ k_i != 0)$ ，否则 $i =i+ 1$

父公钥推导子公钥

$CKDpub((K_{par}, c_{par}), i) → (K_i, c_i)$

检查 $i$ 的值
1. 如果 $i$ 是硬化的（$i ≥ 2^{31}$），则返回失败
2. 否则$I = HMAC-SHA512(Key = c_{par}, Data = ser_P(K_{par}) || ser_{32}(i))$
将 $I$ 等分成两个 32 字节：$I_L$ 和 $I_R$
$K_i = point(parse_{256}(I_L)) + K_{par}$
$c_i = I_R$
$assert(parse_{256}(I_L) < n)$ ，否则 $i =i+ 1$

父私钥推导子公钥

综合上述两个函数，就有两种办法可以实现：

先用 父私钥推导出子私钥，然后用子私钥计算出子公钥
先用父私钥计算出父公钥，然后用 父公钥推导出子公钥 （非硬化的 $i$）

父公钥推导子私钥

无法做到

经典的推导图

读后感

子私钥推导出子公钥

我们这里需要证明的是由父私钥推导出子私钥与父公钥推导出子公钥确实是成对的。也即： $ K_i = k_i G $ ，因为 $K_{par}=k_{par} \cdot G=point(k_{par})$

所以两个函数的计算过程中的 $I$ 其实是相等的，那么就有： \[ \begin{aligned} k_i\cdot G &=(parse_{256}(I_L) + k_{par} (\mod\ n))\cdot G\\ &=parse_{256}(I_L)\cdot G + k_{par}\cdot G (\mod\ n)\\ &=point(parse_{256}(I_L)) + K_{par}\\ &=K_i \end{aligned} \] 原式得证

安全点

如果泄漏了扩展公钥及下面的某个子私钥，那么根据 父公钥推导出子公钥 的方法就可以推导出该泄漏的子私钥下面的所有的孙私钥。更惨的是，子私钥和母链码可以推断出母私钥（但这句话我没有证明）

预防措施就是推导的时候使用硬化因子，即强化衍生。因为在 父公钥推导出子公钥 的方法那里，如果使用的是硬化后的 i，那么是无法推导出子公钥的

所以新的协议使用的 PATH 就是带硬化后的因子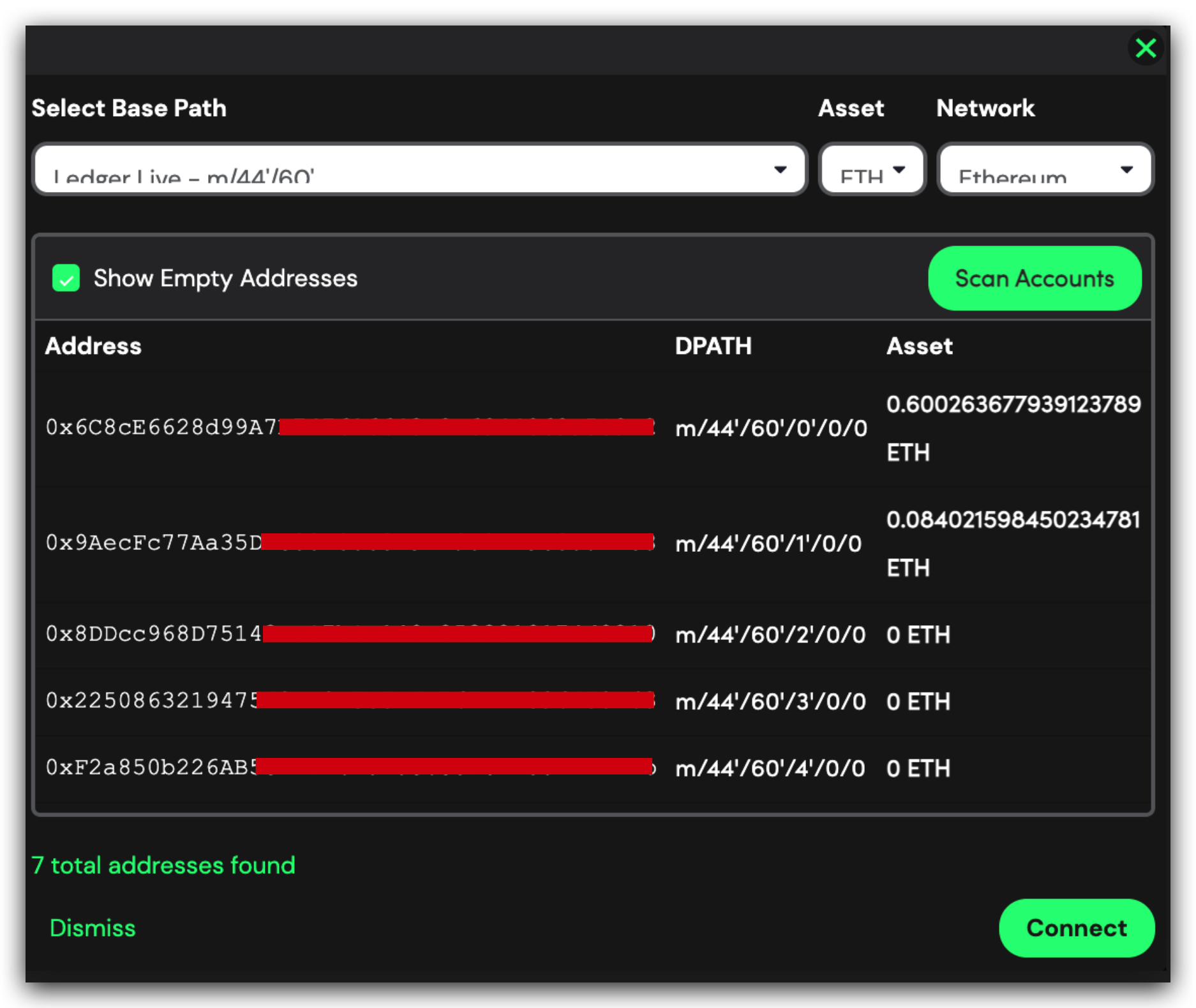： file

而之前旧的协议是没有使用硬化因子的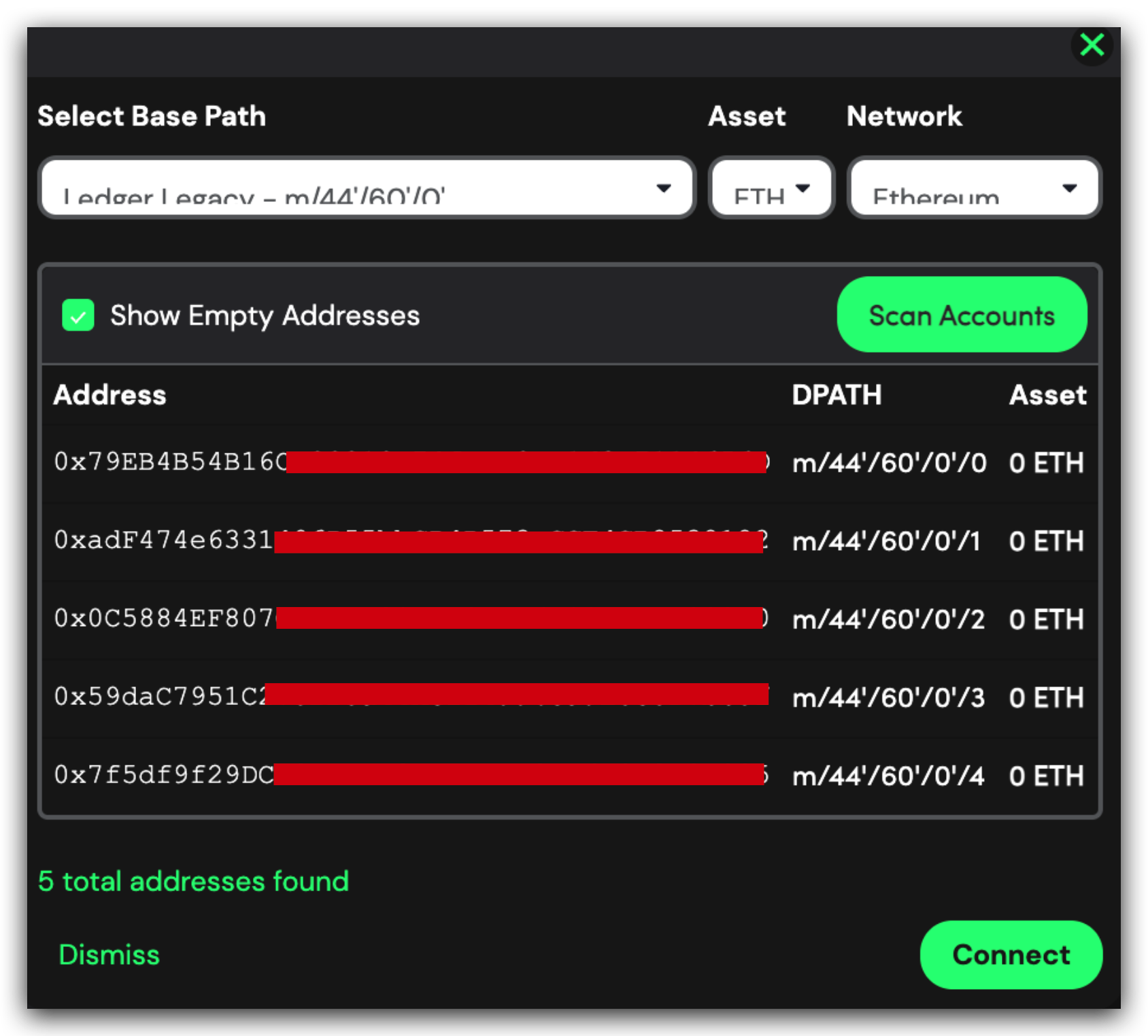： file

BIP39

主要目的

该 BIP 解决了助记词与 entropy 之间的相互转换逻辑的约定俗成

原文精简及读后感

助记词只能是 12、15、18、21、24 个单词，词源总共有 2048 个单词
entropy sha512 之后就是 hd 的主密钥了
entropy 的 bit 位数只能是 128、160、192、224、256。所以这为穷举私钥排除了不少区间（假设绝大部分用户只会用 12 个单词的助记词），但有效的遍历区间依然是个天文数字
entropy 没有校验信息，但助记词是包含校验信息的。也就是说任意一个 128 bit 的随机数都可以推导出一套 12 个单词的助记词，但随意挑选的 12 个单词不一定能组成一套正确的助记词。通常最后一个单词跟校验信息相关，准确地来说是最后半个单词跟校验信息相关，所以如果最后一个单词记不住了，依然很难还原（但暴力穷举例外，毕竟也才遍历 2048 次）
有些用户最开始用的 12 个单词的助记词，后来他自己感觉可能不够安全（其实并没有），希望在不改变收款地址的情况下升级成 24 个单词的助记词。按照现有的方案（bip32、bip39）这个是不可能做到的。

以上内容都总结自 BIP39 的实现源码： Go 版实现和 Python 版实现。两个版本的关键代码我都已经看了：Go 版的精简，易阅读；Python 的夹杂了很多其他功能，再加上语言本身的原因（语法糖很多）如果不清楚需求的话不容易看懂代码。所以想通过源码去理解 BIP39 的同学，建议只去看 Go 版

BIP44

主要目的

该 BIP 解决了从 entropy 推导子孙私钥/公钥逻辑的约定俗成

原文精简及读后感

1	m / purpose' / coin_type' / account' / change / address_index

purpose' 一般是 44' ，因为这是在 BIP44 里提出的（在 BIP49 里面其值是 49）
account' 从 0' 开始递增，一般遵循下列原则
- 如果当前的 account' 没有交易记录那么钱包应用就不应该继续 new 一个新的地址出来（但很多钱包并没有这样实现，至少 metamask 就不是）
- 每次批量生成新的地址时，批量的数字为 20（但很多钱包应用并没有这样实现，比如 gnosis safe 每次是 5 或 7 个）
coin_type' 这个 BIP 里定义了每条链的一个编码，如果是一个公链开发团队且希望其私钥可以支持助记词生成，那么就需要手工去 github 上提 pr 申请

数字的右上角的单引号，就是指硬化因子。其实就是在本身数字的基础上再加上 2^31 就行了。比如 44‘ = 44 + 2^31 = 2147483692。详情可以参看 Python 版的源码：

个人观点总结

后续的很多的协议（BIP39/BIP44/BIP85）都是以 BIP32 为理论基础而拓展出的上层应用协议。然而 BIP32 纯粹就只是一场 math show，看起来用户只需要保存好一个私钥（entropy），省去了管理众多私钥的烦恼，然而过于集权的设计并不值得提倡。

虽然解决了某些场景的使用问题，但同时也挖了不少坑，用户使用的过程中既需要注意这，又需要注意那的，稍微一不注意就容易导致一锅端，或者还没等黑客出手就自己锁死了自己的资产。 BIP39 也是很奇怪的协议，只是把 32 字节的私钥换成了 12～24 个单词，对于普通人来说，依然无法背下来十几二十个单词，大家还是按照对待私钥的方式对待助记词：该截图的截图，该上传的就上传，该抄纸上的抄纸上。

有的人说，如果某个单词抄错了，是可以校验的，而私钥某个字母抄错了不会报错。嗯，确实是这样的，但是助记词虽然有报错，却无法指出是哪一个单词错了，这种报错除了能提前让人进入崩溃状态外起不了什么作用
还有人说，如果一套助记词里的某个字母抄错了（因为会变成一个不存在的英文单词），可以通过少量的穷举恢复正确的助记词出来，而私钥要是某个字母抄错了则毫无办法。嗯，确实是这样，但是这个想法有点既当又立的意思，因为助记词方案本身就是由单词组成的，这样的错误场景有什么好拿得出手来说道的呢？换句话说，我在这里故意挖了一个坑，诶，然后你猜怎么着，我用非常简单的办法又把坑给填上了，你是不是应该夸我这个坑挖得牛逼？🙂️

你在抄写 apple 这个单词的时候，不小心抄成了 appie，难道你发现不出来自己抄错了么，这种一眼就能看出的问题归功于助记词方案上显然有点说不过去。这种错误对比使用私钥就是：抄写私钥的时候把其中某个字母抄成了希腊字母 ∂ ，这是一眼就能看出的错误，这种情况两者都可以通过有限次的穷举就能找出正确答案，但我能说这是私钥这种设计的功劳吗？